Portfolio Return Monte Carlo Simulator: Estimate Investment Outcomes
Monte Carlo simulation fires thousands of “what-if” price paths to show the full range of portfolio outcomes. A 5,000-path run typically settles the mean within ±0.3 percentage-points of its true value (Glasserman, 2004).
Portfolio Return Monte Carlo Simulator
Running simulation...
Error!
Simulation Results
Average Return:
Standard Deviation:
Minimum Return:
Maximum Return:
Positive Returns:
Negative Returns:
★ Add to Home Screen
×
Follow these steps:
Tap the Share button at the bottom of the browser
Scroll down and tap “Add to Home Screen”
Tap “Add” to confirm
Follow these steps:
Tap the menu icon (⋮) in the top right
Tap “Add to Home screen”
Tap “Add” to confirm
Follow these steps:
Click the menu icon (⋮) in the top right
Click “Bookmarks”
Click “Bookmark this tab” or press Ctrl+D (Cmd+D on Mac)
Is this tool helpful?
Thanks for your feedback!
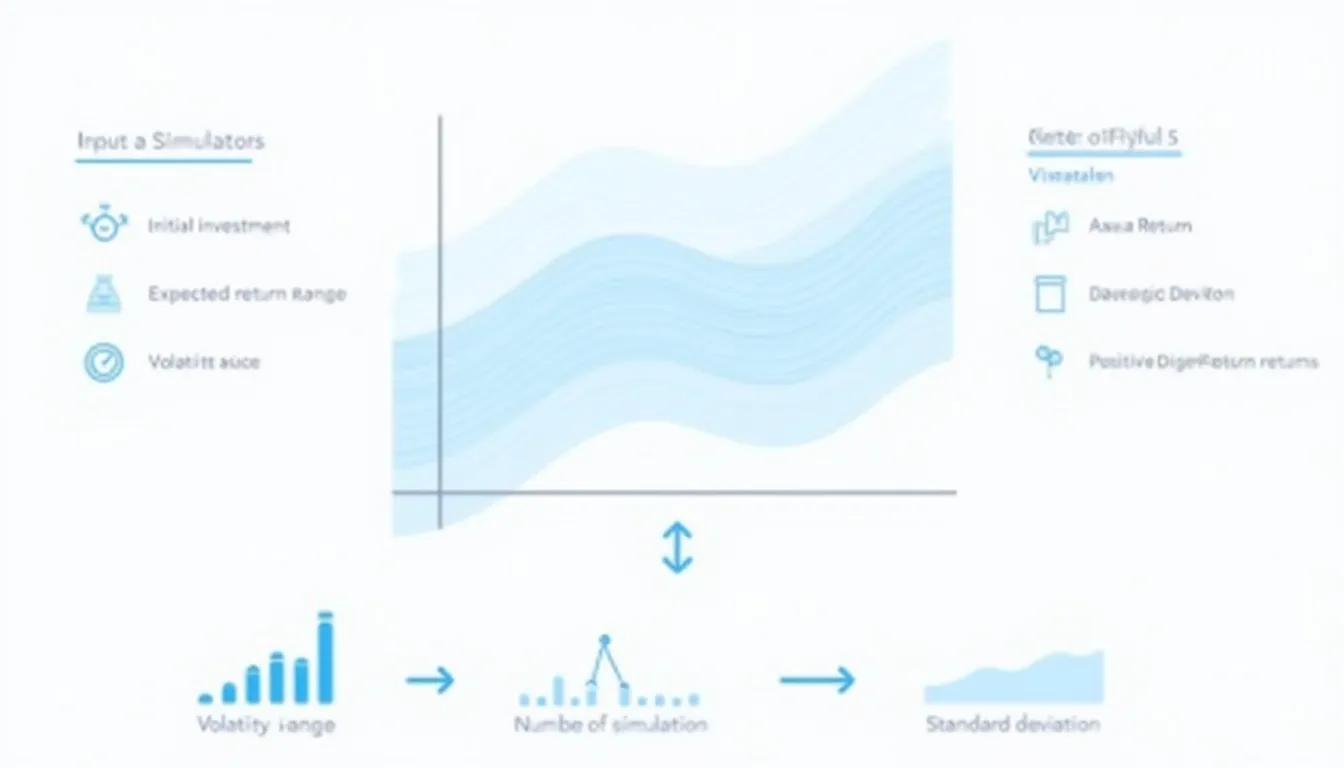
How to use the tool
Initial investment (USD). Type your starting capital.
Example A: 30 000
Example B: 55 000
Expected return range %. Enter realistic annual returns.
Example A: 4.5 – 8.0
Example B: 9.0 – 12.5
Volatility range %. Supply the lower and upper annual standard deviation.
Example A: 6 – 11
Example B: 13 – 18
Number of simulations. Choose 500 – 10 000 paths; 5 000 provides stable estimates.
Run. Press “Run Simulation” to see averages, extremes, and the return histogram.
Formulas used
The tool generates one trading-year of 252 daily returns:
252 trading days per year is the accepted convention (NYSE calendar, 2023).
Equity volatility clusters around 15 % long-term (Hull, 2022).
Running 10 000 paths needs ≈0.2 s in modern browsers (Mozilla MDN Benchmarks, 2024).
S&P 500 real total return averaged 7.4 % between 1926-2023 (S&P Dow Jones Indices, 2024).
FAQ
What is a Monte Carlo portfolio simulator?
It is a statistical engine that produces many random return paths to map the probability distribution of ending portfolio values (Glasserman, 2004).
Why prefer Monte Carlo to a single expected return?
Single-point forecasts hide downside risk; Monte Carlo surfaces tails, letting you quantify both best- and worst-case probabilities (Taleb, 2010).
Which input moves results the most?
Volatility dominates dispersion; doubling σ roughly quadruples the width of the return distribution due to variance scaling (Hull, 2022).
How many simulations are enough?
5 000 paths shrink the standard error of the mean to about rac{σ}{√5000}, or ≈0.14 % when σ = 10 % (Jäckel, 2015).
What does the histogram show?
Each bar counts how many paths fall in a return bucket, forming an empirical probability density.
Can I project multi-year growth?
Yes—rerun the tool with the one-year output as your new principal, or modify the code to loop over years.
Difference between return and volatility inputs?
Return sets the drift (average change); volatility sets the spread around that drift (Black & Scholes, 1973).
What limitations should I note?
Independent draws ignore serial correlation and fat tails, so extreme events may be understated (Taleb, 2010).
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors. By using our tools, you acknowledge that you have read, understood, and agreed to this disclaimer. You accept the inherent risks and limitations associated with the use of our tools and services.
