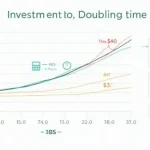
Investment Doubling Calculator: Discover Your Money’s Growth Timeline

Your money doubles when the natural-log formula hits 2. For example, a 7.3 % annual return compounded monthly grows twofold in roughly 9 years 6 months (Finance Formulas, 2023).

Investment Doubling Calculator

Enter the expected annual rate of return as a percentage.

Select how often the investment compounds.

★ Add to Home Screen

Is this tool helpful?

Thanks for your feedback!

How to use the tool

  1. Enter the annual rate of return (%)
    Example 1: 7.3 %. Example 2: 12.4 %.
  2. Select compounding periods per year
    Example 1: 12 = monthly. Example 2: 365 = daily.
  3. Press “Calculate” to display the time—shown in years and months—for the investment to double.

Formula used

Compound-growth doubling time:

$$T = rac{\ln 2}{n \ln\!\left(1+\frac{r}{n}\right)}$$

  • T = years to double
  • r = annual rate (decimal)
  • n = compounding periods per year

Example calculations

  • 7.3 % monthly: $$T \approx rac{0.6931}{12\ln(1+0.073/12)} = 9.5\text{ yrs}$$ ≈ 9 yrs 6 mo.
  • 12.4 % daily: $$T \approx rac{0.6931}{365\ln(1+0.124/365)} = 5.6\text{ yrs}$$ ≈ 5 yrs 7 mo.

Quick-Facts

  • The formula derives from continuous compounding mathematics (Finance Formulas, 2023).
  • Average S&P 500 annualised return since 1926 is ~10 % (Damodaran, 2023).
  • SEC defines daily compounding as 365 periods a year (Investor.gov, SEC 2022).
  • The Rule of 72 gives a rough estimate by 72 / r % (Investopedia, 2023).

FAQ

What does the calculator compute?

It returns the exact years and months needed for an investment to double using your rate and compounding inputs.

Why is natural logarithm used?

Logarithms isolate time in the exponential growth equation, making the doubling point solvable (OpenStax Math, 2021).

Does more frequent compounding always help?

Yes, but gains taper; shifting from monthly to daily cuts less than 1 % off doubling time at common rates (Morningstar, 2022).

How accurate is it versus the Rule of 72?

The Rule of 72 is within ±1 year for 6-10 % rates; the calculator stays exact to the decimal (Graham, 1973).

Can I include taxes and inflation?

Adjust the rate to a real, after-tax figure—e.g., 7 % nominal becomes ~4.5 % real at 2.5 % inflation (BLS CPI, 2023).

Is it useful for debts?

You can invert the sign of the rate, but specialised amortisation calculators handle repayments more realistically (FDIC, 2022).

What if returns vary yearly?

Insert the expected geometric mean return; the tool assumes a constant rate throughout the period (CFA Institute, 2020).

Any quick mental check?

Divide 70 by your rate—for 7 % you get ~10 years—then compare to the precise output to spot data entry errors.

Important Disclaimer

The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. Do not enter personal data, sensitive information, or personally identifiable information in our web forms or tools. Such data entry violates our terms of service and may result in unauthorized disclosure to third parties. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors.

Create Your Own Web Tool for Free

Discover how quickly your investments can double with our easy-to-use Investment Doubling Time Calculator infographic.

Related Tools: