Force Calculator: Easily Compute Newton’s Second Law of Motion
Unlock the power of physics with our interactive Force Calculator! Discover how mass and acceleration interact, explore weight on different planets, and visualize force relationships through dynamic graphs. Perfect for students, engineers, and curious minds alike. Ready to master Newton's Second Law? Dive in now!
Force Calculator
Result:
How to Use the Force Calculator Effectively
Our Force Calculator is a powerful tool designed to help you calculate force using Newton’s Second Law of Motion. Here’s a step-by-step guide on how to use it effectively:
1. Enter the Mass
In the “Mass” field, input the mass of the object you’re calculating force for.
Choose the appropriate unit from the dropdown menu: kilograms (kg), grams (g), or pounds (lb).
Example: For a car, you might enter “1500” and select “kg”.
2. Input the Acceleration
In the “Acceleration” field, enter the acceleration value.
Select the unit of acceleration: meters per second squared (m/s²) or feet per second squared (ft/s²).
Example: For a car accelerating from 0 to 60 mph in 6 seconds, you might enter “4.47” and select “m/s²”.
3. Use Preset Accelerations (Optional)
If you’re calculating weight (force due to gravity) on different celestial bodies, use the “Preset Acceleration” dropdown.
Options include Earth gravity (9.80665 m/s²), Moon gravity (1.62 m/s²), Mars gravity (3.71 m/s²), and Jupiter gravity (24.79 m/s²).
Selecting a preset will automatically fill in the acceleration field.
4. Calculate the Force
Click the “Calculate Force” button to perform the calculation.
The result will be displayed in Newtons (N) and pound-force (lbf).
5. Interpret the Results
The primary result is shown in Newtons, the SI unit for force.
An additional result in pound-force is provided for convenience.
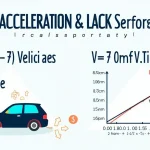
A graph will be generated, showing how force changes with varying mass for the given acceleration.
Understanding Force and Its Calculation
Force is a fundamental concept in physics that describes the interaction between objects. It’s what causes an object to accelerate, decelerate, or change direction. Our Force Calculator is based on Newton’s Second Law of Motion, which states that the force acting on an object is equal to the mass of the object multiplied by its acceleration.
The Mathematical Formula
The formula for calculating force is:
$$F = m \times a$$
Where:
F = Force (measured in Newtons, N)
m = Mass (measured in kilograms, kg)
a = Acceleration (measured in meters per second squared, m/s²)
Purpose and Benefits of the Force Calculator
The Force Calculator serves several purposes and offers numerous benefits:
Quick and Accurate Calculations: It eliminates the need for manual calculations, reducing the chance of errors.
Educational Tool: Students and educators can use it to understand the relationship between mass, acceleration, and force.
Unit Flexibility: It allows inputs in various units, making it useful for users familiar with different measurement systems.
Visualization: The generated graph helps users understand how force changes with varying mass.
Versatility: It can be used for various applications, from simple physics problems to complex engineering calculations.
Benefits of Using the Force Calculator
1. Time-Saving
Manual force calculations can be time-consuming, especially when dealing with multiple scenarios or unit conversions. Our calculator streamlines this process, allowing you to obtain results instantly.
2. Accuracy and Precision
By eliminating human error in calculations, the Force Calculator ensures highly accurate results. This is particularly important in scientific research, engineering projects, and educational settings where precision is crucial.
3. Educational Value
For students learning about Newton’s laws of motion, this calculator serves as an interactive tool to explore the relationship between mass, acceleration, and force. The visual representation through graphs enhances understanding of these concepts.
4. Unit Conversion Simplification
The calculator handles unit conversions automatically, allowing users to input values in their preferred units without worrying about conversion factors. This feature is especially useful for international collaborations or when working with different measurement systems.
5. Versatility in Applications
From calculating the force needed to move furniture to determining the thrust required for rocket propulsion, this calculator is applicable in various fields including physics, engineering, astronomy, and everyday problem-solving.
6. Accessibility and Convenience
Being web-based, the Force Calculator is accessible from any device with an internet connection, making it a convenient tool for students, professionals, and enthusiasts alike.
Addressing User Needs and Solving Specific Problems
Problem 1: Calculating Weight on Different Planets
Many users are curious about how much they would weigh on different celestial bodies. Our Force Calculator addresses this need by providing preset acceleration values for Earth, Moon, Mars, and Jupiter.
Example Calculation:
Let’s calculate the weight of a 70 kg person on Mars:
Mass: 70 kg
Acceleration: 3.71 m/s² (Mars gravity, selected from presets)
The force required is 5205 N or approximately 1170 lbf.
Problem 3: Force in Elevator Systems
Building engineers and physics students often need to calculate forces in elevator systems. Our calculator can help determine the force exerted by an elevator’s motor.
Example Calculation:
Calculate the force needed for an elevator weighing 1000 kg (including passengers) to accelerate upwards at 2 m/s²:
The elevator motor needs to exert a force of 11810 N or about 2655 lbf.
Practical Applications of the Force Calculator
1. Physics Education
Teachers and students can use the Force Calculator to:
Verify homework solutions
Explore how changing mass or acceleration affects force
Understand the concept of weight as a force on different planets
2. Engineering and Design
Engineers can utilize the calculator for:
Determining the force required for machinery operations
Calculating structural loads in building design
Estimating propulsion requirements in aerospace engineering
3. Sports Science
Sports scientists and coaches can apply the Force Calculator to:
Analyze the forces involved in various athletic movements
Optimize training regimens based on force requirements
Study impact forces in contact sports
4. Everyday Problem Solving
The general public can use the calculator for:
Estimating the force needed to move furniture
Calculating the impact force of falling objects
Understanding the forces at play in various household appliances
5. Astronomy and Space Exploration
Astronomers and space enthusiasts can employ the calculator to:
Compare gravitational forces on different planets and moons
Calculate the thrust required for spacecraft launches
Estimate the force of impact for meteors
Frequently Asked Questions (FAQ)
Q1: What is force, and why is it important?
Force is a fundamental concept in physics that describes the interaction between objects. It’s crucial because it explains how objects move, change direction, or maintain their position. Understanding force is essential in various fields, from engineering and sports to everyday activities.
Q2: Can I use this calculator for objects in free fall?
Yes, you can use this calculator for objects in free fall. For objects falling near Earth’s surface (neglecting air resistance), use the acceleration due to gravity, which is approximately 9.81 m/s². You can select this from the preset accelerations in the calculator.
Q3: How do I convert between Newtons (N) and pound-force (lbf)?
The calculator automatically provides results in both Newtons (N) and pound-force (lbf). However, if you need to convert manually:
1 N ≈ 0.224809 lbf
1 lbf ≈ 4.44822 N
Q4: Why does the calculator ask for mass instead of weight?
The calculator uses mass because it’s a constant property of an object, regardless of its location. Weight, on the other hand, is a force that depends on the local gravitational acceleration. By inputting mass, you can calculate force (including weight) under various acceleration conditions.
Q5: Can this calculator be used for calculating friction force?
While this calculator is primarily designed for Newton’s Second Law, it can be adapted for friction calculations. For kinetic friction, you would input the mass of the object and use the coefficient of friction multiplied by the acceleration due to gravity (9.81 m/s²) as your acceleration value.
Q6: How accurate are the preset acceleration values for different planets?
The preset acceleration values provided are widely accepted approximations used in scientific calculations. They are accurate enough for most practical purposes and educational demonstrations. For highly precise scientific work, more exact values might be necessary.
Q7: Can I use this calculator for objects moving in circular motion?
Yes, you can use this calculator for objects in circular motion. In this case, the acceleration would be the centripetal acceleration, which is v²/r, where v is the velocity and r is the radius of the circular path. Input this value as the acceleration in the calculator.
Q8: Is there a maximum or minimum value for mass or acceleration that I can input?
The calculator can handle a wide range of values, from very small to very large. However, for extremely large or small values, consider using scientific notation to input the numbers (e.g., 1e6 for 1,000,000).
Q9: How does changing the mass or acceleration affect the force?
Force is directly proportional to both mass and acceleration. This means:
Doubling the mass while keeping acceleration constant will double the force.
Doubling the acceleration while keeping mass constant will also double the force.
Doubling both mass and acceleration will quadruple the force.
The graph generated by the calculator helps visualize these relationships.
Q10: Can this calculator be used for calculating thrust in rocket science?
Yes, this calculator can be used to calculate thrust in basic rocket science problems. In rocketry, thrust is a force that propels the rocket forward. You would input the mass of the rocket and its acceleration to calculate the thrust force required. However, for more complex rocket calculations involving changing mass (due to fuel consumption) and variable acceleration, more specialized tools might be necessary.
By addressing these common questions, we hope to enhance your understanding and usage of the Force Calculator. Whether you’re a student, educator, engineer, or simply curious about the forces at work in the world around you, this tool provides a quick and accurate way to explore the fundamental principles of physics.
Important Disclaimer
The calculations, results, and content provided by our tools are not guaranteed to be accurate, complete, or reliable. Users are responsible for verifying and interpreting the results. Our content and tools may contain errors, biases, or inconsistencies. We reserve the right to save inputs and outputs from our tools for the purposes of error debugging, bias identification, and performance improvement. External companies providing AI models used in our tools may also save and process data in accordance with their own policies. By using our tools, you consent to this data collection and processing. We reserve the right to limit the usage of our tools based on current usability factors. By using our tools, you acknowledge that you have read, understood, and agreed to this disclaimer. You accept the inherent risks and limitations associated with the use of our tools and services.
